Marking Maths, Part 2

We’ve worked on entering mathematical equations; that’s straightforward, though very hard to do in a way that feels natural on a computer. Harder still is marking such an equation; by which we mean comparing it to a known answer to see if it’s equal.

‘Equal’ here has to be defined carefully and is sometimes split into two categories. There’s syntactically equal expressions - where we say $x + y$ is equal to $y + x$, because they are both just adding $x$ and $y$ together and the order in addition doesn’t matter. Then there’s semantically equal expressions - where $(x + y)^2$ equals $x^2 + 2xy + y^2$ say, or $\frac{1}{\pi}$ equals $\frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{k!^{4}(396^{4k})}$.

Checking semantic equality is hard; in fact it’s known to be impossible in general (see Richardson’s Theorem) – but we’ve never been ones to listen to that sort of thing!

We use SymPy to do the checking; it’s an open-source computer algebra library for Python with excellent support for precisely the equality checking we want. There are quite a few hurdles we had to cross to integrate SymPy into Isaac: it’s Python but Isaac is Java; it can be quite slow sometimes; it checks Python expressions, not LaTeX or a syntax tree directly; and worst of all it’s far too good at what it does (see the image below). It’s amazing at semantic equality; but sometimes we just want syntactic equality!

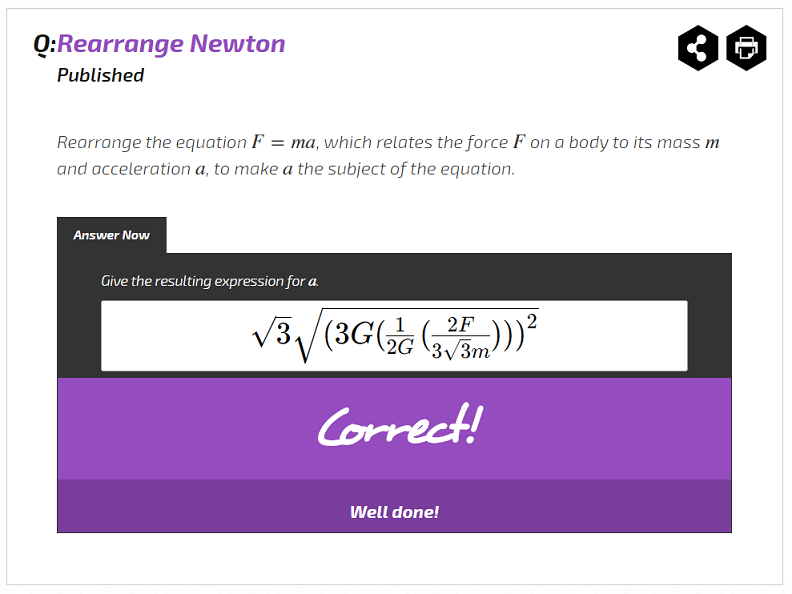
Actually, as a fun aside, SymPy didn’t match the complicated entry in the image to the expected answer of $\frac{F}{m}$: it says they’re not equal. Not because it couldn’t check it, it turns out - but because it assumes everything is a complex number and so $\sqrt{x^{2}} \neq x$. This highlights another issue: Does SymPy say two expressions aren’t equal because they really aren’t equal – or because it can’t simplify them well enough? So I added code to sample the functions at random points of their inputs^[1] and see if the results matched up to within a very small numerical error. It won’t be right every time; but it will flag up possible matches for a human to review.

We then built into the system a way to check syntactic equality too. This turns out to be really useful when we want to make sure someone has factorised an expression – the factorised correct answer is (semantically) equal to the wrong non-factorised answer! Computers don’t yet understand these subtleties.

It’s being slowly rolled out: there are some beta questions which use the checker, and we hope for lots more questions on Isaac to use it soon enough!

^[1] If you’re paying close attention you’ll notice that the expected answer contains the variables $F$ and $m$, but that the thing submitted contains $G$ too. It’s obvious to a person that $G$ cancels out immediately; but not to the computer. So we have to be able to sample $n$ and $m$ dimensional space and compare. Fun!